Electric Fields's Definition
Electric fields play a crucial role in understanding the behavior of charged particles and form the foundation of various scientific principles.
what is electric fields
An electric fields is a force field that surrounds electrically charged particles, exerting influence on other charged particles within its range. This phenomenon is described by the concept of electric force, which acts on any charged object placed within the field.
Some properties of electric field
Gravitational and electric field are long range forces ( Newton and Coulomb)
According to the theory of proportionality, the electric field generated by a positive charge is oriented away from that charge, while the electric field created by a negative charge is directed toward that charge.
We talk about a real electric field. What is electric field then electric field is a force experienced by a unit charge and that unit charge is called test charge.
Let's see what is the electric field due to the point charge
Let's assume that we have to shope bubble first one A which is given a positive charge and the second one is B which has given a negative charge so find out what is the radius or diameter of those bubbles ?
Ans r and 2r respectively and radius will be increase.
A glass rod rubbed with silk and used to charge a gold leaf electroscope and leaf are also observed to Divorce electroscope thus charged is exposed to x-axis for a start period then ?
A cylindrical conductor replaced near and other positively charged conductor the net charge acquired by the cylinder conductor will be ?
Two identical spheres carrying charges - 9 micro coulomb and 5 microcoulomb respectively are kept in contact and then separated from each other point out through a statement for the following ? net charge on both.
Four charges are arranged at the corner of a square ABCD the force on the charge q kept at the center zero is ?
0 b) along AB a) along BD b) along BC c) 0
learn more :
- electric field and application (in easy way )
- electric force most important concepts with examples
- charge density (linear, area, volume with most helpful important examples )
- in-depth about charge with experiments
- what is electric flux: know every things about it with iits examples
- Application of gauss law
The charges -q1 + Q2 and Q3 Are placed on the X component of the force on -q is proportional to ?
q2/b2 - q3/a2sin@
q2/b2 - q3/a2cos@
q2/b2+q3/a2sin@
Superposition principle for electric field
As we know what is electric field.
So E = F/q = kq1*q2/q1*r^2 = kq2/r^2
And electric force in the form of electric field
F = E*Q = kq1*Q/r^2
If we want to measure a net electric field by a different charge particle then we have to use the superposition principle. The net electric field of all charged particles is the vector addition of
individual electric fields.
Find out the electric field at the center ?
If any charges are removed on vertex or not same then net E.F will be non zero.
Null point
The point at which net electric field or net electric force becomes zero is called null point and at that point electric force experienced by that charge particle or that particle which is present at that point is zero .
find out null points ?
Graphical representation of null points
Case 1 when both charges are same or like
Case 2 when both charges are opposite or unlike
Note
if charges are equal but unlike then there is a non null point exist
and if charges are unlike and one is greater than other So null point may exist near to large charge .
If charges are equal but unlike then there is no null point exist.
Motion of a charge in electric field
Uniform electric field :
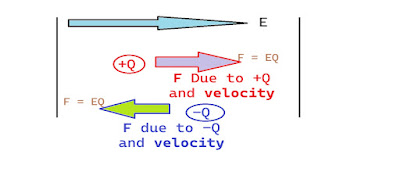
When a charged entity encounters a consistent electric field, it is subject to a force arising from said field. The force's orientation aligns with the electric field's direction and the charge's sign. Expressing this force (F) acting on the charge (q) involves Coulomb's Law:
[ F = qE ]
In this equation:
( F) denotes the force on the charge,
( q ) represents the particle's charge,
( E ) stands for the electric field.
For positively charged particles, the force aligns with the electric field. Conversely, for negatively charged particles, the force opposes the electric field's direction.
The acceleration (a) experienced by the charged particle is calculable through
Newton's second law (F = ma):
[ F = ma ]
This translates to the acceleration (a) being given by:
[ a = F/m]
where (m) denotes the mass of the charged particle.
Should the charged particle initiate motion with an initial velocity (v0), its subsequent movement can be delineated using the equations of motion. In the presence of a uniform electric field, the velocity of the charged particle (v) exhibits a linear evolution concerning time:
[ v = v0 + at ]
Here, (t) signifies the time elapsed.
For a charged particle starting from rest (v0 = 0), the velocity as a function of time becomes:
[ v = at ]
The position (x) of the charged particle over time finds expression in:
[ x = x0 + v0 t + ½ a t^2 ]
In this equation, (x0) denotes the initial position.
Within a uniform electric field, a charged particle's motion is characterized by constant acceleration, and the aforementioned equations aptly depict its behavior.
Some most important questions:
electric field formula
Or
electric field intensity formula
Or
formula of electric field
Or
formula of electric field intensity
Or
intensity of electric field
Or
define electric field intensity
Or
what is electric field intensity
Or
electric field formula class 12
Or
electric field intensity definition
Ans:->
The electric field (E) or electric field strength at a specific point in space is defined as the force (F) experienced by a positive test charge (q) located at that point, divided by the magnitude of the test charge. Mathematically, this relationship is expressed by the formula:
[ E = F/q ]
In this formula:
(E) represents the electric field or electric field strength,
(F) is the force encountered by the test charge,
(q) denotes the magnitude of the test charge.
Expressed in volts per meter (V/m), electric field intensity (E) is the unit of measurement derived from the formula.
For a point charge (Q) positioned at a distance (r), the electric field intensity can be articulated as:
[ E = k Q/ r^2]
Here:
(E) signifies the electric field intensity,
(k) stands for Coulomb's constant (\(8.99 \times 10^9 \, \text{N m}^2/\text{C}^2\)),
(Q) represents the charge, and
(r) denotes the distance from the charge.
In the realm of Class 12 physics, students frequently encounter these equations when delving into electrostatics. The electric field concept offers insights into comprehending the impact of a charged object on the surrounding space.
si unit of electric field
Or
unit of electric field
Or
electric field unit
Or
unit of electric field intensity
Or
electric field intensity unit
Or
si unit of electric field intensity
Ans:-> The SI unit of electric field or electric field intensity is the volt per meter (V/m).
define electric field
Or
electric field definition
Or
electric field class 12
Or
electric field is scalar or vector
Or
electric field definition class 12
Or
what is electric field class 12
Ans:->
The electric field at a specific point in space is a vector quantity describing the force encountered by a positive test charge positioned at that point. It signifies the force per unit positive charge and is denoted by the symbol (E). Mathematically, the electric field (E) at a point is articulated through the formula:
[ E = F/q]
In this expression:
- (E) denotes the electric field,
- (F) represents the force experienced by a positive test charge,
- (q) is the magnitude of the test charge.
When considering a point charge (Q) at a distance (r) from the source, the electric field (E) can be denoted as:
[ E = KQ / r^2]
Here:
- (k) stands for Coulomb's constant (8.99 * 10^9 , {N m}^2/{C}^2),
- (Q) denotes the charge, and
- (r) signifies the distance from the charge.
The electric field is a vector due to its possession of both magnitude and direction. The direction of the electric field at a point aligns with the direction in which a positive test charge would undergo a force. In the domain of Class 12 physics, students explore electric fields as a component of their study in electrostatics.
properties of electric field lines
Or
properties of electric field
Or
electric field lines
Or
direction of electric field
Or
what is electric field lines
Or
what are electric field lines
Or
electric field direction
Or
electric field lines class 12
Or
define electric field class 12
Ans:-
The characteristics of electric field lines play a crucial role in comprehending the intricacies of the electric field. Here are pivotal features to consider:
1. Origin and Termination:
- Electric field lines initiate from positive charges and conclude at negative charges. They don't commence or conclude in open space.
2. Direction:
- The orientation of electric field lines aligns with the force experienced by a positive test charge. They emanate from positive charges and converge towards negative charges.
3. Spacing:
- The density of electric field lines reflects the intensity of the electric field. Proximity indicates a robust field, while greater spacing signifies a weaker electric field.
4. Perpendicular to Conductors:
- Electric field lines are consistently perpendicular to the surface of conductors in a state of equilibrium. This characteristic ensures an absence of electric field components inside a conductor during electrostatic equilibrium.
5. No Intersecting Lines:
- Electric field lines never cross paths. Intersection would imply a point in space experiencing conflicting electric field directions, which is physically illogical.
6. Uniform Electric Field:
- In a uniform electric field, lines are straight and evenly distributed. This indicates a constant magnitude and direction of the electric field strength.
7. Divergence:
- The quantity of electric field lines entering or exiting a surface correlates with the net charge enclosed. This principle is articulated in Gauss's law for electricity.
8. Closed Loop Behavior:
- Electric field lines cannot form closed loops. They extend infinitely or culminate at a charge. This absence of closed loops stems from the conservative nature inherent in electric fields.
Grasping these electric field line properties is vital for visualizing and scrutinizing electric fields in diverse configurations.
dimension of electric field
Or
electric field dimensional formula
Or
dimensional formula of electric field
Or
electric field dimension
Ans:->
The dimensional formula for the electric field (E) in terms of fundamental physical dimensions is articulated as follows:
(E) = [M1 L1 A-1 T-3]
Here, the symbols represent the fundamental dimensions:
- (M) for mass,
- (L) for length,
- (T) for time,
- (A) for electric current.
This formula is derived from the fundamental dimensions of force (([F] = M^{1} L^{1} T^{-2}) and charge ([Q] = A T). The electric field, defined as force per unit charge, manifests its dimensional formula as an expression of dependence on mass, length, time, and electric current.
relation between electric field and potential
Or
relation between electric field and electric potential
Ans:->
The correlation between the electric field (E) and electric potential (V) is expressed through the following equation:
[ E = -dV/dr ]
In this equation:
- (E) signifies the electric field,
- (V) represents the electric potential,
- (r) denotes the distance from the source of the electric field,
- (dV/dr) conveys the rate of change of electric potential concerning distance.
In simpler terms, this equation asserts that the electric field at a specific point is equivalent to the negative of the rate of change of electric potential concerning distance at that specific point. This fundamental relationship highlights that electric field lines align with the direction of the steepest decline in electric potential.
Alternatively, the connection can be articulated as:
[ V = - ∫E dr]
[ V = - E r]
[ E = - V/r]
Here, the electric potential (V) at a point equals the negative of the integral of the electric field (E) concerning distance (r) from a reference point. This equation provides a method for calculating the electric potential at a given point based on the electric field along the pathway.
These expressions are pivotal for comprehending the interplay between electric field and electric potential within the realm of electrostatics.
Learn more:
- Electric force : with experiment of daily life and in-depth analysis
- electric field with amazing examples
Learn more excitement topics:
learn more :
- electric field and application (in easy way )
- electric force most important concepts with examples
- charge density (linear, area, volume with most helpful important examples )
- in-depth about charge with experiments
- what is electric flux: know every things about it with iits examples
- Application of gauss law










